


Cred ca la inceput de saptamana cand nici iarba nu creste, un imbold primit din partea unor probleme de logica ar fi binevenit pentru “demarajul” mintal necesar unei noi saptamani. Sper sa fiti mai inspirati decat sunt eu lunea.
Problema 1
Taiati tabla de mai jos in 4 parti egale astfel incat fiecare parte sa contina cate un cal.
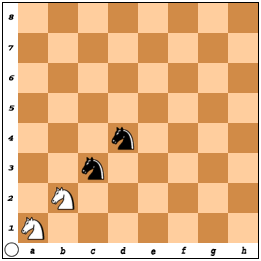
Problema 2
Putem afla volumul corespunzator unui anumit numar de bile care se afla intr-un vas gradat?
Problema 3
Putem afla volumul unei sticle umplute mai putin de jumatate cun lichid, care are fundul circular sau dreptunghiular numai cu ajutorul unui metru? (nu este permisa golirea sau umplerea sticlei).
Problema 4
Daca cineva care face diferenta dintre un numar de 3 cifre nesimetric si acelasi numar rasturnat va spune ultima cifra a acestei diferente, puteti afla care este diferenta celor 2 numere?
Problema 5
Trei frati trebuiau sa imparta 24 de mere, si fiecare a primit un numar de mere echivalent cu varsta fiecaruia cu 3 ani in urma. Cel mic a propus o alta metoda de impartire:
“Voi pastra numai jumatate din merele pe care le am, si le voi imparti pe celelalte intre voi, in mod egal. Dar dupa aceea fratele meu mijlociu va trebui sa imparta si el jumatate din merele pe care le are, intre fratele meu mai mare si mine, in mod egal, iar dupa aceea fratele mai mare va trebui sa faca acelasi lucru.”
Toti au fost de acord, iar in final fiecare a avut cate 8 mere. Ce varsta aveau fratii?














5 Comentarii
Problema 5.
Varstele fratilor: 7 ani, 10 ani, 16 ani.
Problema 4.
Diferenta dintre un numar XYZ (cu cifrele X,Y,Z) si rasturnatul lui (adica ZYX) este
XYZ-ZYX=99*(X-Z).
Ultima cifra a diferentei este 10-(X-Y), deci aceasta cifra determina doar diferenta X-Y si nicidecum numarul XYZ.
Problema 3.
Putem determina aria bazei prin masurarea directa a diametrului (daca e circulara) sau a lungimilor laturilor (daca e dreptunghiulara). Inaltimea lichidului poate fi masurata pe langa sticla (daca e transparenta) sau prin scufundarea capatului metrului in lichid pana la fundul sticlei (vedem pana la ce nivel se uda). Inmultind aria bazei cu inaltimea, obtinem volumul cautat. Nota: S-au facut presupuneri “normale” cum ar fi cea ca toate sectiunile orizontale ale partii pline a sticlei au aceeasi arie ca baza (sticla nu se ingusteaza).
Problema 2.
martie 29, 2010 - 4:34 pmTurnam apa in vas pana acoperim bilele. Citim volumul indicat de gradatii, apoi scoatem bilele (lasand apa) si citim din nou volumul. Volumul bilelor este dat de diferenta valorilor citite.
@ Vlad
Problemele 2 si 5 sunt corect rezolvate.
La problema 3 se cere volumul sticlei si nu al lichidului din ea (presupunerile “normale” sunt corecte). Aici poate ar fi trebuit sa spun ca sticla are dop 🙂 .
La problema 4 o sa mai las enuntul o perioada de timp, pentru ca exista totusi o solutie.
martie 29, 2010 - 8:12 pmProblema 3.
Putem afla si volumul sticlei in felul urmator. Mai intai determinam aria bazei “S”, inaltimea “h” a lichidului din sticla si volumul S*h ocupat de lichid. Pe urma intoarcem sticla cu dopul in jos si masuram inaltimea “H” a portiunii goale a sticlei. Volumul sticlei va fi
V=S*h+S*H=S(h+H).
Acum s-a presupus ca in sticla rasturnata lichidul ocupa toata portiunea ingustata dinspre dop, astfel incat portiunea ramasa libera este cilindrica sau paralelipipedica.
Problema 4.
martie 29, 2010 - 8:54 pmDin ultima cifra “C” a diferentei XYZ-ZYX nu putem afla numerele XYZ si ZYX, ci doar diferenta insasi. Diferenta are cifrele:
9-C (sute), 9 (zeci), C (unitati).
De exemplu, daca cineva porneste de la XYZ=572 si ne spune doar ultima cifra C=7 a diferentei, putem deduce ca diferenta este 297. Aceeasi diferenta se obtine si pornind de la XYZ=734 (si de la multe alte numere). Deci nu putem determina “cele doua numere” (cum cere problema) ci doar diferenta lor.
E corect si P3.
martie 29, 2010 - 8:57 pmLa P4 am gresit cand am scris enuntul problemei. Enuntul (corectat acum) cerea sa se afle diferenta celor 2 numere (scuze, in special lui Vlad, pentru confuzie).
martie 29, 2010 - 9:23 pm