Probleme de logica la inceput de saptamana (43)

40

Cred ca la inceput de saptamana cand nici iarba nu creste, un imbold primit din partea unor probleme de logica ar fi binevenit pentru “demarajul” mintal necesar unei noi saptamani. Sper sa fiti mai inspirati decat sunt eu lunea.

Problema 1

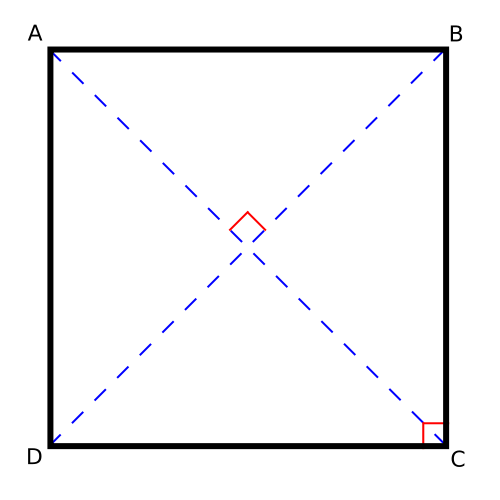
Patru orase, sa le numim A, B, C si D, se afla in colturile unui patrat cu latura de 100 km. Administratia drumurilor a dorit sa le conecteze folosind cea mai scurta posibil retea de drumuri.

-Putem face drumuri directe de la un oras la celalalt. In felul acesta ne-ar fi necesari doar 300 km de drumuri, a propus cineva.

-Am putea face chiar mai bine decat atat. Daca facem drumurile pe cele doua diagonale ne vor trebui doar 200√2 km.

Care este cea mai scurta retea de drumuri, avand in vedere ca nici realizarea drumurilor pe diagonalele patratului nu este solutia corecta?

 

Problema 2

Pe o mica insula un inventator si-a construit o mica baza aeriana, in care a realizat cateva avioane care se alimenteaza cu un carburant special, care a fost produs de catre acesta pe insula. Pentru a-si face reclama acesta a decis sa realizeze o calatorie circulara in jurul Pamantului fara sa mai aterizeze intr-un alt loc. Problema era ca rezervoarele avioanelor nu puteau sa ia decat cantitatea de combustibil necesara pentru a face jumatate din drum. Orice cantitate de carburant putea fi insa transferata fara probleme, in zbor, dintr-un rezervor in altul al avioanelor. Pentru scopul problemei se presupune ca nu se pierde timp cu alimentarea, nici in aer, nici pamant.
Care este cel mai mic numar de avioane necesar pentru realizarea calatoriei, presupunand ca avioanele au aceeasi viteza constanta si acelasi consum de combustibil, si ca toate se intorc in siguranta pe insula?

Problema 3

Cinci barbati si o maimuta care au naufragiat pe o insula pustie si-au petrecut prima zi culegand nuci de cocos pentru hrana, pe care le-au asezat intr-o gramada, si, fiind prea obositi ca sa le imparta atunci, s-a udus la culcare, urmand sa faca lucrul acesta a doua zi. Unul dintre ei s-a trezit nu a putut sa doarma, cu teama ca ar putea fi pacalit de catre ceilalti, asa ca s-a dus la gramada, a impartit in 5 nucile de cocos, si, cum i-a ramas una, i-a dat-o maimutei, dupa care s-a dus si si-a ascuns partea lui, dupa care s-a dus si s-a culcat.

Al doilea s-a trezit noaptea cu o teama similara, si a procedat ca si primul, si tot ca si el, dupa impartire i-a ramas o nuca de cocos, pe care i-a dat-o maimutei, etc. Acelasi lucru s-a petrecut cu toti cei 5 oameni.

Dimineata, dupa trezire, au impartit nucile de cocos ramase la 5 (de data aceasta, impartirea nu a mai dat rest).

Cate nuci de cocos au fost la inceput?

Problema 4

O cantitate foarte mare de benzina se afla la marginea unui desert cu o latime de 800 km, dar nu exista nicio sursa de carburant in interiorul acestuia. Un camion poate cara destul combustibil pentru a strabate 500 km (vom numi aceasta cantitate “un rezervor”), si isi poate face propriile “statii de realimentare” de-a lungul drumului lasand combutibil in canistre de-a lungul acestuia. Se presupune ca nu exista pierderi cauzate de evaporare din aceste recipiente.

Care este cantitatea de combustibil (in “rezervoare”) necesara pentru traversarea desertului? Exista vreo limita a latimii desertului pe care ar putea sa-l strabata un camion?

Problema 5

Ultima problema este una de amuzament, si are enuntul:

Albul muta si da mat in 4 mutari