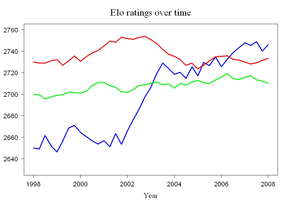
De cand FIDE a anuntat propriile sale intentii cu privire la creşterea factorilui K, există brusc o preocupare acerba în jurul acestui subiect. Se pare ca atat suporteri ai acestei schimbari precum GM Bartlomiej Macieja cat şi adversari precum GM John Nunn au argumente puternice. Acest lucru ar putea fi confuz pentru cineva care nu s-a gandit niciodata cu adevărat la această temă, dar chiar dacă aufacut-o, nu este surprinzător. Într-un comentariu, statisticianul Daan Zult lamureste niste aspecte legate de acest subiect.
Cu putin timp in urma FIDE a exprimat temerile ei despre efectele noului factor K, care va intra in vigoare de la 1 iulie, şi a decis să publice în paralel cele două liste de evaluare timp de un an, iar apoi de revizuiasca rezultatele diferitilor factori K în vigoare. GM Bartlomiej Macieja a făcut apel puternic la decizia de a nu întârzia, si de a creşte factorul K imediat. Ulterior FIDE a trimis o declaratie de presa, care a fost urmata de un alt răspuns din partea lui Macieja. În acelaşi timp, GM John Nunn a exprimat un alt punct de vedere, spunând că “se pare că nu exista nici o dovadă că factorul K – 20, va avea drept rezultat un sistem de evaluare mai precis, în acelasi timp existand o serie de riscuri şi dezavantaje.”
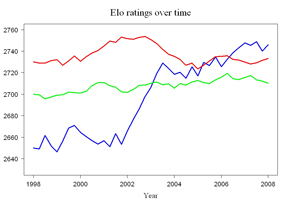
Am lucrat cu modelul ELO ca si statistician in scopuri psihologice şi am am fost nevoit de multe ori sa fac o alegere corecta a factorului K. Alegerea este întotdeauna între precizie şi viteza de modifcare: atunci când daţi factorului K o valaore mica, ratingul se va schimba lent şi este mai puţin fluctuat, daca se da factorului K o valoare mare, ratingul se va modifica si fluctua mai rapid şi mai mult. Acest lucru poate fi un lucru bun, dacă un jucător de şah nu mai face progrese reale în calitatea jocului. De exemplu, fiecare jucător de şah probabil stie un jucator care a fost destul de talentat ca si junior, dar dintr-un motiv s-a oprit din a mai progresa la un anumit punct. O oprire a crestii progresului trebuie sa se stabilizeze în jurul unui anumit rating, şi nu într-un clasament care face fluctuaţii mari. Alegerea K-factor este, prin urmare, o alegere între două rele şi între două bunuri, ca o sticlă jumatate plina sau jumătate goala. Pentru a lamurii anumite aspecte, voi discuta unele argumente care le-am întâlnit recent.
 GM John Nunn
GM John Nunn
Cea mai recentă contribuţie la discuţie a fost cea a lui GM Dr. John Nunn de pe site-ul Chessbase. Nunn se intreba unde este dovada că un factor K de de24, comparativ cu valoarea curentă de 10 va avea ca rezultat mai multă acurateţe in anticiparea rezultatelor viitoare ale jucătorilor. Pentru mine, întrebarea sa vine ca o mica o surpriza, deoarece autorul initial al propunerii unui factor K-24, Jeff Sonas, susţine declaraţia sa cu dovezi empirice într-un articol care a aparut de asemenea pe Chessbase în anul 2002. Sonas a analizat rezultatele a 266.000 jocuri, şi a comparat rezultatele reale, cu rezultatele care au fost anticipate de ratingul ELO. El arată că în conformitate cu valoarea curentă a factorului previziunile nu sunt exact similare cu rezultatele reale. De exemplu, în concordanta cu formula ELO, un jucător care are 150 de puncte rating mai mult decât adversarul său , se asteapta la un scor de 70%. Sonas arată că, ori de câte ori un jucator are 150 de puncte mai mult decât adversarul său, el obtine un punctaj de 68% în loc de 70%. De asemenea, el arată că, atunci când vom folosi un factor K-24, rezultatele a 266.000 jocuti s-ar putea anticipa mai bine decât sunt acum. În general argumentatia lui Sonas este puternică, pentru că nu se bazeze doar pe baza teoretica, dar de asemenea, dar si pe argumente empirice.
O a doua obiecţie, care a fost adusa de Nunn se referă la un argument prezentat de către GM Bartlomiej Macieja, care afirmă că o creştere a factorului K- este un rezultat logic al faptului că FIDE actualizeaza noi liste de evaluare pe baze mult meu regulate. Nunn, pe de altă parte, afirmă că factorul K şi frecvenţa de actualizare a listelor de evaluare a ratingului sunt fără nici o legătură intre ele. Această declaraţie este mai mult sau mai puţin corecta, dar el sustine acesta afirmatie cu argumente greşite. Nunn afirmă că, atunci când cineva joaca 40 de jocuri în termen de şase luni, nu ar trebui să existe diferenţe în lista FIDE publicata la fiecare şase luni sau una publicata zilnic. El ar fi avut dreptate dacă sunt actualizare as-ar difacut dupa fiecare meci, dar în actualul system de calculal ratingului FIDE, declaraţia este incorecta. La articolul 14.4 din regulamentele FIDE putem citi că FIDE nu actualizeaza rating dupa fiecare meci, doar după o serie de jocuri jucatet într-o perioadă.
FIDE afirmă că actualizarea după fiecare meci ar face ratingul mai exact, dar nu o pot realiza, pentru că este o muncamultprea complexa. Un alt motiv bun pentru a nu actualiza ratingul după fiecare meci, fără publicarea unui nou clasament după fiecare meci, este faptul că o schimbare în clasament va fi, apoi, bazata pe ratinguri virtuale. Aceasta este o problema, pentru ca apoi jucătorii nu pot calcula noul lor rating, după un turneu, pentru că adversarul său ar putea avea un alt rating virtual decât ratingul de pe lista de rating.
 GM Bartlomiej Macieja
GM Bartlomiej Macieja
O altă problemă cu actualizarea rating, după fiecare meci se referă la turneele închise. Când organizatorii doresc să organizeze un turneu de o anumită categorie, sau un turneu pentryu realizarea de norme IM sau GM, este important ca ratingul jucatorilor invitati sa fie fix şi cunoscut. Astfel, există suficiente motive pentru a nu actualiza ratingul după fiecare meci, deşi acesta ar putea deveni mai clar. Dar sa ma intorc la subiect, vreau sa ilustrez o greseala în argumentele lui Nunn pritr-un exemplu simplu:
Să presupunem că avem doi jucători, un jucător A cu un rating de 2000 şi jucător B cu un rating de 2100. Să presupunem că ei joacă 40 de meciuri in 6 luni, şi ca fiecare meci se termină remiza. Acum, să comparam ceea ce se întâmplă atunci când recalculam ratingul, după fiecare meci sau după toate cele 40 de meciuri. În primul rând, atunci când ratingul este calculate dupa fiecare meci, jucatorul A va câştiga puncte şi jucătorul B va pierde puncte. După un anumit număr de jocuri ratingul celor doi va fi 2050. Cu toate acestea, atunci când ratingul este calculat după 40 de meciuri, atunci noul rating al jucătorului A va fi:
2000 (= votarea curentă)
+ 40 (= # jocuri)
* 20 (= k-factor)
* (0,5 (= scor real)
– 0.36 (= scorul anticipat, pe baza formulei ELO)
= 2112 (= noul rating).
Se observa ca s-a întâmplat ceva ciudat. Un jucator cu un rating de 2000, care a jucat 40 de remize împotriva unuia cu rating 2100, acum are un rating de 2112!? Observam ca actualizarea după fiecare meci rezultata un rating diferit (şi, mai exact), decât atunci când se actualizeaza după fiecare şase luni.
Cu toate acestea, această caracteristică nu va dispărea când vom modifica valoarea factorului K, deci, în acest sens Nunn are dreptate cand spune că factorul K independent de numărul de liste deactualizare. Macieja se refera la faptul ca, atunci când listele de actualizare apar mai frecvent, este mai greu sa cresti in clasament. Aceasta este, de asemenea, adevărat, pentru că atunci când ratingul este în creştere, şi clasamentul este actualizat mai des, obti unrating mai mare si este nevoie sa joci chiar mai bine pentru a obţine mai multe puncte. Totusi, ceea ce Macieja nu menţionează , este faptul ca un numar de liste mai mare, de asemenea introduce si ratinguri volatile. Când ratingul este actualizat la fiecare şase luni, există posibilitatea unui jucător să repare un turneu slab cu un turneu normal mai târziu, astfel încât ratingul sa nu se schimbe prea mult. În timp ce în conformitate cu o actualizare mai frecventă un turneu slab va avea ca rezultat o scadere de rating, care ar putea să nu fie reprezentativ pentru talentul sau. Aceasta înseamnă că idea unei actualizari mai frecventa a listelor de rating poate fi, de asemenea, utilizata ca un argument teoretic, pentru a susţine o scădere a factorului K
După cum putem vedea, teoretic discuţiei nu oferă o soluţie clară. În astfel de situaţii este bine sa lăsam dovezile empirice sa vorbeasca. Până în prezent, numai simgura lucrare empirica cu privire la acesta problema este furnizata de către Jeff Sonas. Activitatea sa, oferă o bază solidă pentru a începe discuţia. El a arătat, în mod clar că un factor K-24 ar duce la un rating cu o putere de predicţie mai precisă. Totusi, calculele sale se referă la un numar mare de jucători de şah. Mi se pare că ratingul jucatorilor de top merită o atenţie specială, peca ei reprezinta lume sahului ca un sport. Pentru ca este destul de probabil ca, la nivel de vârf, fi=orta dejoc se schimba mai lent, prin urmare, este posibil ca o creştere a factorului K sa conduca la previziuni mai puţin precise ale rezultatelor jucatorilor de top. Dacă acest lucru este adevărat sau nu nu poate fi răspuns fără o investigatie empirica, care până acum nu a fost realizata.
Ca o notă personală aş dori să adaug că o altă soluţie pentru această problemă ar fi de a asigura un model complet nou pentru clasament. Modelul ELO a fost realizat în 1960, într-un timp în care calculele necesare sa faceau fără calculator. Prin urmare modelul ELO este atât elegant cat şi primitiv. În zilele noastre, sunt disponibile modele mai complexe şi mai precise. O caracteristică importantă a modelelor mai avansate este că ele determina factorul K la nivel individual. Deoarece disponibilitatea calculatoarelor nu mai este o problemă şi calculul cu precizie a rating a devenit mai important, utilizarea de modele mai avansate de calcul al ratingului ar putea fi important de luat in seama.











0 Comentarii